Giải bài toán bằng cách lập phương trình| Toán 8 chương trình mới

Giải việc bằng phương pháp lập phương trình là phần kiến thức và kỹ năng phổ cập nhập lịch trình toán 8 trình bày riêng biệt và bậc học tập trung học cơ sở trình bày công cộng. Theo dõi nội dung bài viết nhằm biết phương pháp lập phương trình và giải những dạng việc tương quan nằm trong VUIHOC.

1. Phương pháp giải việc bằng phương pháp lập phương trình toán 8

- Các bước giải việc bằng phương pháp lập phương trình toán 8:

Bạn đang xem: Giải bài toán bằng cách lập phương trình| Toán 8 chương trình mới

+ Cách 1: Lập phương trình

Chọn ẩn số và bịa đặt ĐK tương thích cho tới ẩn số ê.
Biểu thao diễn những đại lượng chưa chắc chắn theo dõi ẩn số và những đại lượng tiếp tục biết.
Lập phương trình biểu thị quan hệ trong số những đại lượn.

+ Cách 2: Giải phương trình

+ Cách 3: Kết luận nghiệm của phương trình đem thỏa mãn nhu cầu ĐK ko.

- Lưu ý Khi lựa chọn ĐK cho tới ẩn:

+ Ẩn được lựa chọn là đại lượng đem nhập câu hỏi

+ Nếu biểu thị ẩn x là một trong chữ số => 0 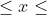$\leq x\leq$ 9

+ Ẩn x vẹn toàn dương nếu như biểu thị cho tới tuổi tác, người, thành phầm...

+ Biểu thị véc tơ vận tốc tức thời => ẩn x > 0.

2. Các dạng bài bác phần mềm giải bài bác toàn bằng phương pháp lập phương trình

2.1 Dạng việc đem động

Với dạng việc vận động, những em cần thiết cảnh báo một số trong những điều sau:

quãng lối = véc tơ vận tốc tức thời × thời gian
vận tốc xuôi dòng sản phẩm = véc tơ vận tốc tức thời Khi nước tĩnh lặng + véc tơ vận tốc tức thời dòng sản phẩm nước
vận tốc ngược dòng sản phẩm = véc tơ vận tốc tức thời Khi nước tĩnh lặng - véc tơ vận tốc tức thời dòng sản phẩm nước

2.2 Dạng việc năng suất

Trong quy trình ngơi nghỉ năng suất, những em cần thiết chú ý:

Có tía đại lượng nhập cuộc là: Toàn cỗ việc làm, phần việc làm thực hiện được nhập một đơn vị chức năng thời hạn (năng suất) và thời hạn.
Nếu một nhóm thực hiện kết thúc việc làm nhập x ngày thì một ngày team ê thực hiện được 1/x việc làm.
Xem toàn cỗ việc làm là 1 trong (công việc).
Khối lượng việc làm = Năng suất × Thời gian

2.3 Dạng việc lần số

Với việc dạng tím số, những em cần thiết lưu ý:

2.4 Dạng việc hình học

Với việc hình dạng học tập, những em cần thiết ghi ghi nhớ những kiến thức và kỹ năng sau:

a. Hình chữ nhật đem 2 cạnh là a và b thì diện tích S của hình chữ nhật là a.b,

Chu vi của hình chữ nhật là 2(a + b)
Diện tích: a.b

b. Hình vuông đem cạnh vày a thì

Diện tích hình vuông vắn là a²,
Chu vi của hình vuông vắn là 4a

c. Tam giác có tính lâu năm tía cạnh thứu tự là a, b, c, lối cao h

Diện tích: (h.đáy)/2
Chu vi: a+b+c

>> Xem thêm: Tổng phù hợp kiến thức và kỹ năng toán 8 cụ thể SGK mới

3. Bài tập giải việc bằng phương pháp lập phương trình toán 8

3.1 Bài tập luyện giải việc bằng phương pháp lập phương trình toán 8 liên kết tri thức

Bài 7.7 trang 35 SGK toán 8/2 liên kết tri thức

Gọi lộc mỗi tháng của chị ấy Linh là x (triệu đồng) (0 < x < 290).

=> thưởng Tết của chị ấy Linh là 2,5x (triệu đồng).

Lương 12 mon của chị ấy Linh là 12x (triệu đồng).

Theo đề bài bác tao đem phương trình: 12x + 2,5x = 290 $\Leftrightarrow$ 14,5x = 290 $\Leftrightarrow$ x = trăng tròn (thỏa mãn).

Vậy lộc mỗi tháng của chị ấy Linh là trăng tròn triệu đồng.

Bài 7.8 trang 35 SGK toán 8/2 liên kết tri thức

Gọi số chi phí chưng Hưng dùng để làm mua sắm trái khoán công ty là x (triệu đồng).

Điều kiện: 0 ≤ x ≤ 300.

Khi ê số chi phí chưng Hưng dùng để làm gửi tiết kiệm ngân sách ngân hàng là 300 – x (triệu đồng).

Số chi phí lãi chưng Hưng chiếm được kể từ mua sắm trái khoán công ty là 0,08x (triệu đồng) và số chi phí lãi chiếm được kể từ gửi tiết kiệm ngân sách ngân hàng là 0,06(300 – x) (triệu đồng).

Theo đề bài bác tao đem phương trình: 0,08x + 0,06(300 – x) = 22 $\Leftrightarrow$ 0,08x + 18 – 0,06x = 22

$\Leftrightarrow$ 0,02x = 4 $\Leftrightarrow$ x = 200 (thỏa mãn)

Vậy chưng Hưng sử dụng 200 triệu để sở hữ trái khoán và sử dụng 100 triệu nhằm gửi tiết kiệm ngân sách ngân hàng.

Bài 7.9 trang 36 SGK toán 8/2 liên kết tri thức

Gọi x (triệu đồng) là niêm yết của từng cái TV loại A. Điều khiếu nại 0 < x < 36,8.

=> niêm yết của từng cái tủ giá buốt loại B là 36,8 – x (triệu đồng).

Vì TV loại A được hạn chế 30% => giá buôn bán của từng cái TV loại A sau thời điểm hạn chế giá chỉ là 0,7x (triệu đồng).

Tương tự động, vì thế tủ giá buốt loại B được hạn chế giá chỉ 25% => giá cả của từng cái tủ giá buốt loại B sau thời điểm hạn chế giá chỉ là 0,75(36,8 – x) (triệu đồng).

Theo đề bài bác tao đem phương trình: 0,7x + 0,75(36,8 – x) = 26,805 $\Leftrightarrow$ 0,7x + 27,6 – 0,75x = 26,805

$\Leftrightarrow$ –0,05x = 26,805 – 27,6 $\Leftrightarrow$ x = 15,9 (thỏa mãn)

Vậy niêm yết của từng cái TV loại A là 15,9 triệu đồng, niêm yết của từng cái tủ giá buốt loại B là 36,8 – 15,9 = trăng tròn,9 triệu đồng.

Bài 7.10 trang 36 SGK toán 8/2 liên kết tri thức

Gọi thời hạn dịch rời của Nam là x (giờ) (x > 0).

Khi ê, quãng lối Nam lên đường được là 12x (km).

Nam tách căn nhà khi 14 giờ và Hùng cho tới căn nhà Nam khi 14 giờ 10 phút nên Hùng dịch rời nhằm đuổi theo kịp Nam sau Nam 10 phút, tức là 1616 giờ.

Thời gian lận dịch rời của Hùng là 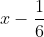$x-\frac{1}{6}$ (giờ).

Quãng lối Hùng lên đường được là 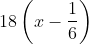$18\left ( x-\frac{1}{6} \right )$ (km).

Theo đề bài bác, tao đem phương trình:

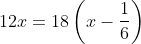
$12x=18\left ( x-\frac{1}{6} \right )$

$\Leftrightarrow$ 18x – 12x = 3 $\Leftrightarrow$ 6x = 3

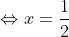$\Leftrightarrow x=\frac{1}{2}$ (thỏa mãn).

Ta đem $\frac{1}{2}$ giờ = nửa tiếng.

Vậy Hùng đuổi theo kịp Nam khi 14 giờ nửa tiếng.

Bài 7.11 trang 36 SGK toán 8/2 liên kết tri thức

a) Ta đem 900 đồng = 0,9 ngàn đồng; 700 đồng = 0,7 ngàn đồng.

Số chi phí cần trả nhập mon Khi dùng gói cước của doanh nghiệp A là

32 + 0,9x (nghìn đồng).

Số chi phí cần trả nhập mon Khi dùng gói cước của doanh nghiệp B là

38 + 0,7x (nghìn đồng).

b) Theo đề bài bác, tao đem phương trình: 32 + 0,9x = 38 + 0,7x $\Leftrightarrow$ 0,2x = 6 $\Leftrightarrow$ x = 30.

Vậy với nửa tiếng gọi thì số chi phí cần trả nhập mon Khi dùng công ty của nhì doanh nghiệp viễn thông này là như nhau.

3.2 Bài tập luyện giải việc bằng phương pháp lập phương trình toán 8 chân mây sáng sủa tạo

Bài 1 trang 39 SGK toán 8/2 chân mây sáng sủa tạo

Gọi số lô hàng phó trong thời gian ngày loại nhất là x (0 < x < 95)

Số đơn phó trong thời gian ngày loại nhì là 95 – x (đơn)

Số đơn phó trong thời gian ngày loại nhì nhiều hơn nữa ngày loại nhất là 15 đơn nên tao đem phương trình:

(95 – x) – x = 15 $\Leftrightarrow$ –2x = 15 – 95 $\Leftrightarrow$ –2x = –80 $\Leftrightarrow$ x = 40 (thỏa mãn)
Vậy số đơn phó trong thời gian ngày loại nhất là 40 đơn.

Bài 2 trang 39 SGK toán 8/2 chân mây sáng sủa tạo

Gọi thời hạn bơi lội là a (phút) (0 < a < 40)

Thời gian lận chạy cỗ là 40 – a (phút)

Số năng lượng tiêu hao cho tới bơi lội và chạy cỗ thứu tự là:

14a; 10(40 – a) = 400 – 10a (calo)

Tổng số năng lượng tiêu hao là 500 nên tao có:

14a + 400 – 10a = 500 $\Leftrightarrow$ 4a + 400 = 500 $\Leftrightarrow$ 4a = 100

$\Leftrightarrow$ a = 25 (thỏa mãn)

Suy đi ra thời hạn bơi lội là: 25 phút

Thời gian lận chạy cỗ là: 40 – 25 = 15 (phút)

Vậy thời hạn chạy cỗ của người sử dụng Bình là 15 phút.

Bài 3 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Gọi số gạo bán tốt trong thời gian ngày loại nhất là x kg (x > 560)

Số gạo bán tốt trong thời gian ngày loại hai: x – 560

Nếu ngày loại nhất bán tốt thêm thắt 60 kilogam gạo thì tiếp tục cấp 1,5 chuyến ngày loại nhì nên tao đem phương trình:

x + 60 = 1,5(x − 560) $\Leftrightarrow$ x + 60 = 1,5x – 840 $\Leftrightarrow$ –0,5x = –900

$\Leftrightarrow$ x = (–900) : (–0,5) $\Leftrightarrow$ x = 1800 (thỏa mãn)

Vậy ngày loại nhất bán tốt 1800 kilogam gạo.

Bài 4 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Ta có: 5 giờ 24 phút = 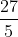$\frac{27}{5}$ giờ

Gọi chừng lâu năm quãng lối AB là x (km) (x > 0)

Thời gian lận người ê lên đường kể từ A cho tới B là 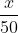$\frac{x}{50}$ giờ.

Thời gian lận người ê lên đường kể từ B về A là 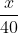$\frac{x}{40}$ giờ

Thời gian lận cả lên đường và về là 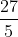$\frac{27}{5}$ giờ, tao đem phương trình:

$\frac{x}{50}+\frac{x}{40}=\frac{27}{5}$

$\Leftrightarrow$ 4x + 5x = 1080 $\Leftrightarrow$ 9x = 1080

$\Leftrightarrow$ x = 120 km (thỏa mãn)

Vậy quãng lối AB lâu năm 120 km.

Bài 5 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Gọi số chi phí nhưng mà chưng Năm mang theo gửi là x đồng. Điều kiện: x>0

Vì lãi vay là 6,2%/năm nên số chi phí lãi sau năm loại nhất chưng năm cảm nhận được là:

x.6,2% = x.0,062(đồng)

Số chi phí cả gốc lẫn lộn lãi của chưng Năm sau năm loại nhất là x+0,062x = 1,062x (đồng)

Số chi phí lãi chưng Năm cảm nhận được ở năm loại nhì là:

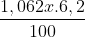
$\frac{1,062x.6,2}{100}$

Số chi phí cả gốc và lãi sau năm loại nhì là:

$1,062x+\frac{1,062x.6,2}{100}$

Vì số chi phí chưng Năm chiếm được cả gốc và lãi sau hai năm là 225 568 800 đồng nên tao đem phương trình:

$1,062x+\frac{1,062x.6,2}{100}=225568000$

$\Leftrightarrow \frac{1,062x.100}{100}+\frac{1,062x.6,2}{100}=\frac{225568000.100}{100}$

$\Leftrightarrow$ 1,062x.100 + 1,062x.6,2 = 225568800.100

Xem thêm: Hướng dẫn cắt ảnh trên PC bằng nhiều cách

$\Leftrightarrow$ 106,2x + 6,5844x= 22556880000

$\Leftrightarrow$ 112,7844x=22556880000

$\Leftrightarrow$ x = 22556880000:112,7844

$\Leftrightarrow$ x= 200000000(thỏa mãn điều kiện)

Số chi phí ban sơ chưng Năm gửi tiết kiệm ngân sách là 200 000 000 đồng.

Bài 6 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Gọi số học viên khối 8 là x em (0 < x < 580)

Số học viên khối 9 là 580 – x (em)

Số học viên xuất sắc khối 8 là 0,4x (em)

Số hoc sinh xuất sắc khối 9 là 0,48(580 – x)

Tổng số học viên xuất sắc là 256 em nên tao đem phương trình:

0,4x + 0,48(580 – x) = 256

$\Leftrightarrow$ 0,4x + 278,4 – 0,48x = 256

$\Leftrightarrow$ –0,08x = –22,44

$\Leftrightarrow$ x = 280 (thỏa mãn)

Vậy số học viên khối 8 là 280 em, số học viên khối 9 là 580 – 280 = 300 (em).

Bài 7 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Gọi x (g) là lượng hỗn hợp ban đầu (x > 0).

Lượng muối hạt nhập hỗn hợp ban sơ là 0,12x (gam)

Pha thêm thắt 350g nước, tao đem x + 350 (gam)

Tỉ lệ Xác Suất muối hạt nhập hỗn hợp mới nhất vày 0,05(x + 350)

Vì lượng muối hạt bất biến nên tao đem phương trình là:

$\Leftrightarrow$ 0,12x = 0,05(x + 350) $\Leftrightarrow$ 0,12x = 0,05x + 17,5

$\Leftrightarrow$ 0,07x = 17,5 $\Leftrightarrow$ x = 250 (thỏa mãn)

Vậy lượng hỗn hợp nhập lọ khi đầu là 250g.

Bài 8 trang 40 SGK toán 8/2 chân mây sáng sủa tạo

Gọi x (đồng) là giá chỉ từng số năng lượng điện ở tầm mức loại nhất (x > 0).

Khi ê, tao có:

Giá từng số năng lượng điện ở tầm mức 2 là: x + 56 (đồng)
Giá từng số năng lượng điện ở tầm mức 3 là: x + 56 + 280 = x + 336 (đồng)
Giá từng số năng lượng điện ở tầm mức 4 là : x + 336 + 522 = x + 858 (đồng)

Nhà Minh sử dụng không còn 185 số năng lượng điện = 50 + 50 + 85.

Như vậy căn nhà Minh cần đóng góp cho tới 50 số năng lượng điện ở tầm mức 1, 50 số năng lượng điện ở tầm mức 2 và 85 số năng lượng điện ở tầm mức 3.

Giá chi phí 50 số năng lượng điện nấc trước tiên là: 50x (đồng)
Giá chi phí 50 số năng lượng điện nấc loại nhì là: 50(x + 56) (đồng)
Giá chi phí 85 số năng lượng điện còn sót lại nấc loại tía là: 85(x + 336) (đồng).

Khi ê, số chi phí năng lượng điện (chưa tính VAT) của phòng Cường bằng:

50x + 50(x + 56) + 85(x + 336)

= 50x + 50x + 2 800 + 85x + 28 560

= 185x + 31 360

Thuế VAT căn nhà Cường cần trả là: 0,1(185x + 31 360)

Tổng số chi phí năng lượng điện căn nhà Cường cần đóng góp (tiền gốc + thuế) bằng:

1,1(185x + 31 360)

Thực tế căn nhà Cường không còn 95 700 đồng nên tao đem phương trình:

1,1(185x + 31 360) = 375 969

⇔ 203,5x + 34 496 = 375 969

⇔ 203,5x = 341 473

⇔ x = 1678 (đồng) (thỏa mãn điều kiện).

Vậy từng số năng lượng điện ở tầm mức giá chỉ loại 3 là 1678 + 336 = 2014 (đồng).

3.3 Bài tập luyện giải việc bằng phương pháp lập phương trình toán 8 cánh diều

Bài 1 trang 49 SGK toán 8/2 cánh diều

Vì chúng ta Minh tiếp tục vấn đáp toàn bộ những câu nhập cuộc ganh đua nên chúng ta Minh chỉ hoàn toàn có thể vấn đáp chính hoặc sai.

Gọi số câu chúng ta Minh vấn đáp chính là x(0<x<20, x ∈ ℕ^*)(câu).

Khi ê, số câu chúng ta Minh vấn đáp sai là 20−x (câu).

Số điểm cảm nhận được cho tới câu vấn đáp chính là 5x (điểm).

Số điểm cảm nhận được cho tới câu vấn đáp sai là ‒1.(20 ‒ x) = ‒20 + x (điểm).

Số điểm chúng ta Minh đạt được là: 5x−20+ x (điểm).

Vì chúng ta Minh được 70 điểm nhập cuộc ganh đua nên tao đem phương trình: 5x−20+ x = 70.

Giải phương trình:

5x−20+ x = 70 $\Leftrightarrow$ 6x = 70 + 20

$\Leftrightarrow$ 6x = 90 $\Leftrightarrow$ x = 15 (thỏa mãn điều kiện).

Vậy chúng ta Minh tiếp tục vấn đáp chính được15 câu.

Bài 2 trang 49 SGK toán 8/2 cánh diều

Gọi niêm yết của sản phẩm thanh lọc nước là x (triệu đồng).

Giá niêm yết của nồi cơm trắng năng lượng điện là 6,5−x (triệu đồng).

Giá sau thời điểm hạn chế của sản phẩm thanh lọc nước là (100%−15%).x=85%x = 0,85x (triệu đồng).

Giá sau thời điểm hạn chế của nồi cơm trắng năng lượng điện là:

(100%−10%).(6,5−x)=90%.(6,5 – x) = 0,9.(6,5−x)(triệu đồng).

Theo fake thiết, tao đem phương trình: 0,85x + 0,9.(6,5 − x) = 5,65.

Giải phương trình:

0,85x+0,9.(6,5−x)=5,65 $\Leftrightarrow$ 0,85x + 5,85 ‒ 0,9x = 5,65

0,85x ‒ 0,9x = 5,65 ‒ 5,85 $\Leftrightarrow$ ‒0,05x = ‒0,2

$\Leftrightarrow$ x = ‒0,2 : (‒0,05) $\Leftrightarrow$ x = 4 (thỏa mãn điều kiện) .

Vậy niêm yết của sản phẩm thanh lọc nước là 4 triệu đồng và niêm yết của nồi cơm trắng năng lượng điện là 6,5 ‒ 4 = 2,5 triệu đồng.

Bài 3 trang 49 SGK toán 8/2 cánh diều

Gọi số chi phí ban sơ chưng An gửi nhập ngân hàng là: x (đồng) (x > 0).

Số chi phí sau 1 năm gửi ngân hàng là:

x.(1 + 5,6%) = x.(1 + 0,056) = 1,056x (đồng).

Số chi phí sau 2 năm gửi ngân hàng là:

1,056x(1 + 5,6%) = 1,056x.(1 + 0,056) = 1,056x.1,056 = 1,115136x (đồng).

Theo fake thiết, tao đem phương trình: 1,115136x=111 513 600

Giải phương trình:

1,115136x=111 513 600

$\Leftrightarrow$ x = 111 513 600 : 1,115136

$\Leftrightarrow$ x =100 000 000(thỏa mãn điều kiện).

Vậy ban sơ chưng An tiếp tục gửi nhập ngân hàng số chi phí là 100 000 000đồng.

Bài 4 trang 49 SGK toán 8/2 cánh diều

Gọi quãng lối nhưng mà xe pháo xe hơi chuyên chở đã đi được kể từ Cần Thơ cho tới Bội nghĩa Liêu là x (km), x > 0.

Thời gian lận xe pháo xe hơi chuyên chở lên đường không còn quãng lối là 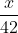$\frac{x}{42}$ (giờ).

Thời gian lận xe pháo xe taxi lên đường không còn quãng lối là 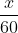$\frac{x}{60}$ (giờ).

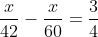
Vì xe pháo xe hơi chuyên chở lên đường trước xe pháo xe taxi 45 phút = $\frac{3}{4}$ giờ nên tao đem phương trình: $\frac{x}{42}-\frac{x}{60}=\frac{3}{4}$

Giải phương trình:

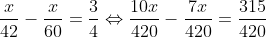
$\frac{x}{42}-\frac{x}{60}=\frac{3}{4}\Leftrightarrow \frac{10x}{420}-\frac{7x}{420}=\frac{315}{420}$

$\Leftrightarrow$ 10x ‒ 7x = 315 $\Leftrightarrow$ 3x = 315

$\Leftrightarrow$ x = 315 : 3 $\Leftrightarrow$ x = 105 (thỏa mãn điều kiện).

Vậy quãng lối xe pháo xe hơi chuyên chở đã đi được kể từ Cần Thơ cho tới Bội nghĩa Liêu là 105 km.

Bài 5 trang 49 SGK toán 8/2 cánh diều

Số vẹn toàn tử O nhập phân tử nitric acid là x (nguyên tử), điều kiện x ∈ ℕ^*.

Khối lượng của x vẹn toàn tử O là 16x (amu).

Khối lượng của một vẹn toàn tử H là 1.1 = 1(amu).

Khối lượng của một vẹn toàn tử N là 14.1 = 14(amu).

Theo fake thiết, tao đem phương trình: 16x + 1 + 14 = 63.

Giải phương trình:

16x + 1 + 14 = 63 $\Leftrightarrow$ 16x = 63 ‒ 1 ‒14

$\Leftrightarrow$ 16x = 48 $\Leftrightarrow$ x = 48 : 16

$\Leftrightarrow$ x = 3 (thỏa mãn điều kiện).

Do ê phân tử của nitric acid ê mang trong mình 1 vẹn toàn tử H, một vẹn toàn tử N và 3 vẹn toàn tử O.

Xem thêm: 99,99% người được hỏi chắc chắn sẽ không biết Mặt trời thực chất có màu gì

Vậy công thức phân tử của nitric acid ê là HNO₃.

Trên đó là bài học kinh nghiệm giải việc bằng phương pháp lập phương trình toán 8 lịch trình mới nhất. Trong khi VUIHOC cũng chỉ dẫn những em cơ hội giải những bài bác tập luyện nhập bài học kinh nghiệm trong số sách toán 8 liên kết trí thức, chân mây tạo ra và cánh diều. Hy vọng rằng qua quýt bài học kinh nghiệm, những em hoàn toàn có thể bắt được cơ hội giải việc bằng phương pháp lập phương trình hàng đầu một ẩn.

>> Mời những em xem thêm thêm: